Julia集

目录
使用 golang 绘制一个朱利亚集合图像。
朱利亚集合
朱利亚集合(Julia Set)是在复平面上点的集合,所以可以使用二维平面绘制出来。
定义1
朱利亚集合可以由下式进行反复迭代得到:
$$ f_c(z) = z^2 + c $$
对于固定的复数 c,取某一 z 值(如 $z_0$),可以得到序列:
$$ z_0, f_c(z_0), f_c(f_c(z_0)), f_c(f_c(f_c(z_0))), \ldots $$
这一序列可能发散于无穷大或始终处于某一范围之内并收敛于某一值。
我们将使其不扩散的 z 值的集合称为朱利亚集合。
理解
- 点的集合
- 满足 $f_c(z)$ 序列收敛的集合(之前我以为是序列的集合)
- 直观上使函数不发散的范围应该是:
$$
\begin{cases}
z = a + bi & a,b=(-1,1)\\
c = d + ei & d,e=(-1,1)
\end{cases}
$$ - 判断点是否趋于收敛条件2是 $|z|<2$
复数
运算法则3
- 加减法
$$
(a+bi)+(c+di)=(a+c)+(b+d)i \\
(a+bi)-(c+di)=(a-c)+(b-d)i
$$ - 乘除法
$$
(a+bi)(c+di)=(ac-bd)+(bc+ad)i \\
\frac{a+bi}{c+di}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i
$$
理解
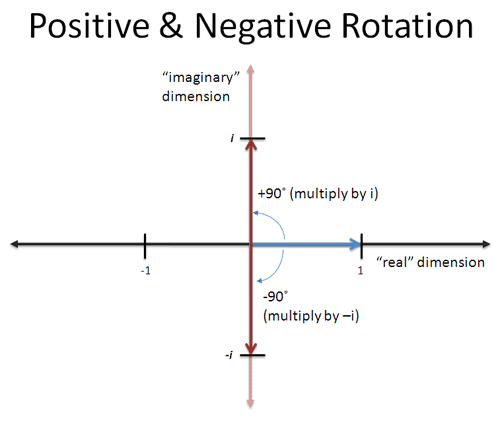
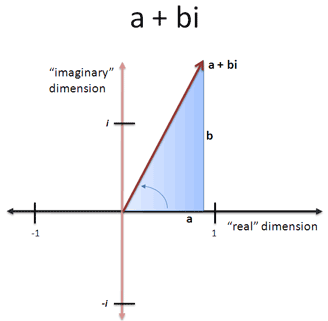
复数包含实部和虚部,也就是长度和旋转量,所以可以用二维平面表示5。
实现
根据复数乘法法则可得到 $f_c(z)$ 函数如下计算,返回新的 $z$ 值。
func julia_fc(zx, zy, cx, cy float64) (float64, float64) {
z_x := zx*zx - zy*zy + cx
z_y := 2*zx*zy + cy
return z_x, z_y
}
迭代 n 次保证 $z$ 值在一定范围内,迭代次数越多(收敛)则点的灰度越小(即暗),迭代次数越少(发散)则点的灰度越大(即亮)。
const (
_JULIA_R = 2.0
)
func julia_divergent_grey(zx, zy, cx, cy float64) int {
for i := 255; i >= 0; i -= 3 {
zx, zy = julia_fc(zx, zy, cx, cy)
if math.Sqrt(zx*zx+zy*zy) > _JULIA_R {
return i
}
}
return 0
}
因为真实的图像坐标是正整数,而 Julia 集收敛坐标在 [-1,1] 之间,所以计算时需要进行一次坐标变换。
最终绘图函数如下,复数 $c$ 值为每次调用随机生成。
func julia(img *image.RGBA, limit int) {
s := rand.NewSource(time.Now().Unix())
r := rand.New(s)
// c = [0, 1]
cx := r.Float64()*2 - 1
cy := r.Float64()*2 - 1
fmt.Println(cx, cy)
for i := 0; i < limit; i++ {
zx := float64(4*i)/float64(limit) - _JULIA_R
for j := 0; j < limit; j++ {
zy := float64(4*j)/float64(limit) - _JULIA_R
gray := uint8(julia_divergent_grey(zx, zy, cx, cy))
point(img, i, j, color.Gray{gray})
}
}
}
测试
func Test_julia(t *testing.T) {
const r = 1000
img := image.NewRGBA(image.Rect(0, 0, r, r))
julia(img, r)
f, _ := os.OpenFile("julia.png", os.O_WRONLY|os.O_CREATE, 0600)
defer f.Close()
png.Encode(f, img)
}
生成一些好看的图像:








停不下来了 …⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄….